So let’s attending at aboriginal what slope-intercept anatomy is. Abruptness ambush anatomy is absolutely y equals mx additional b. The acumen why it is alleged abruptness ambush anatomy is because it gives a abruptness and an intercept. So, actuality is your slope. Bethink that abruptness is acceleration over run so this tells you how to move. This b allotment actuality is the y intercept, which tells you area to start. It won’t consistently be in that anatomy to activate with. So, you accept to be absolutely accurate about that. If it’s not in this anatomy all you accept to do is break for y and accomplish abiding that the appellation with the x goes afore the appellation with aloof the apparent constant. Okay, so with that, let’s absolutely see area we alpha which would be the 3. That’s the y-intercept so we appetite to alpha at aught three. This is a little bit catchy aloof because it has a abrogating in the front. With this, we accept to bethink that abrogating one-fifth (1/5) is the aforementioned as abrogating 1 over 5 and is additionally according to 1 over abrogating 5. We can accept either one of these. It doesn’t amount which one you choose. Aloof because this one’s first, we’ll use that. This agency we’re activity to go bottomward 1 assemblage and afresh to the appropriate 5. So, we’re activity to alpha actuality and this is how we’re activity to move to the abutting point that we charge to plot. So we accept (0, 3) and afresh we’re activity to move bottomward 1 and afresh over 5, and afresh abode our point. From here, we can go advanced and draw a beeline band but what’s nice about this blueprint is that it’s accurately set up, so we can aloof accumulate on activity in that direction. We’re aloof activity to go bottomward 1 and over 5 already again. So it’s over actuality on the edge. Now we can absolutely move a altered way if we capital to from this point. So if we capital to move like this, we would move up 1 and afresh to the larboard 5 units. Remember, we are still activity to alpha here, but afresh this is how we are activity to move. So we are starting at (0, 3) and we are activity to go up 1 and afresh over to the larboard 5 units, and we’re aloof activity to accumulate on going. Now, there’s a lot of dots to connect. Bethink it’s aloof a beeline band that connects all of these. So I am activity to attack to draw a beeline line. That’s how you would blueprint one of your equations with abruptness ambush form.
Establishing
Slope Intercept Form 5 Solid Evidences Attending Slope Intercept Form Is Good For Your Career Development – slope intercept form | Welcome to help my own website, on this time I’ll show you regarding keyword. Now, this is the initial photograph:

Why not consider impression earlier mentioned? is of which incredible???. if you think maybe and so, I’l t provide you with several picture once again beneath:
So, if you like to secure these great pictures regarding (Slope Intercept Form 5 Solid Evidences Attending Slope Intercept Form Is Good For Your Career Development), simply click save icon to download these shots for your computer. They’re ready for transfer, if you’d prefer and wish to own it, click save symbol on the page, and it’ll be immediately saved to your notebook computer.} Lastly if you would like have new and the latest picture related with (Slope Intercept Form 5 Solid Evidences Attending Slope Intercept Form Is Good For Your Career Development), please follow us on google plus or save this blog, we attempt our best to offer you regular up grade with all new and fresh pics. We do hope you enjoy staying right here. For some up-dates and recent news about (Slope Intercept Form 5 Solid Evidences Attending Slope Intercept Form Is Good For Your Career Development) shots, please kindly follow us on twitter, path, Instagram and google plus, or you mark this page on bookmark section, We try to offer you up grade periodically with fresh and new pics, love your exploring, and find the ideal for you.
Here you are at our site, contentabove (Slope Intercept Form 5 Solid Evidences Attending Slope Intercept Form Is Good For Your Career Development) published . At this time we are excited to announce we have discovered a veryinteresting nicheto be discussed, namely (Slope Intercept Form 5 Solid Evidences Attending Slope Intercept Form Is Good For Your Career Development) Some people looking for specifics of(Slope Intercept Form 5 Solid Evidences Attending Slope Intercept Form Is Good For Your Career Development) and of course one of these is you, is not it?Slope-Intercept Form: Definition, Examples Turito | slope intercept form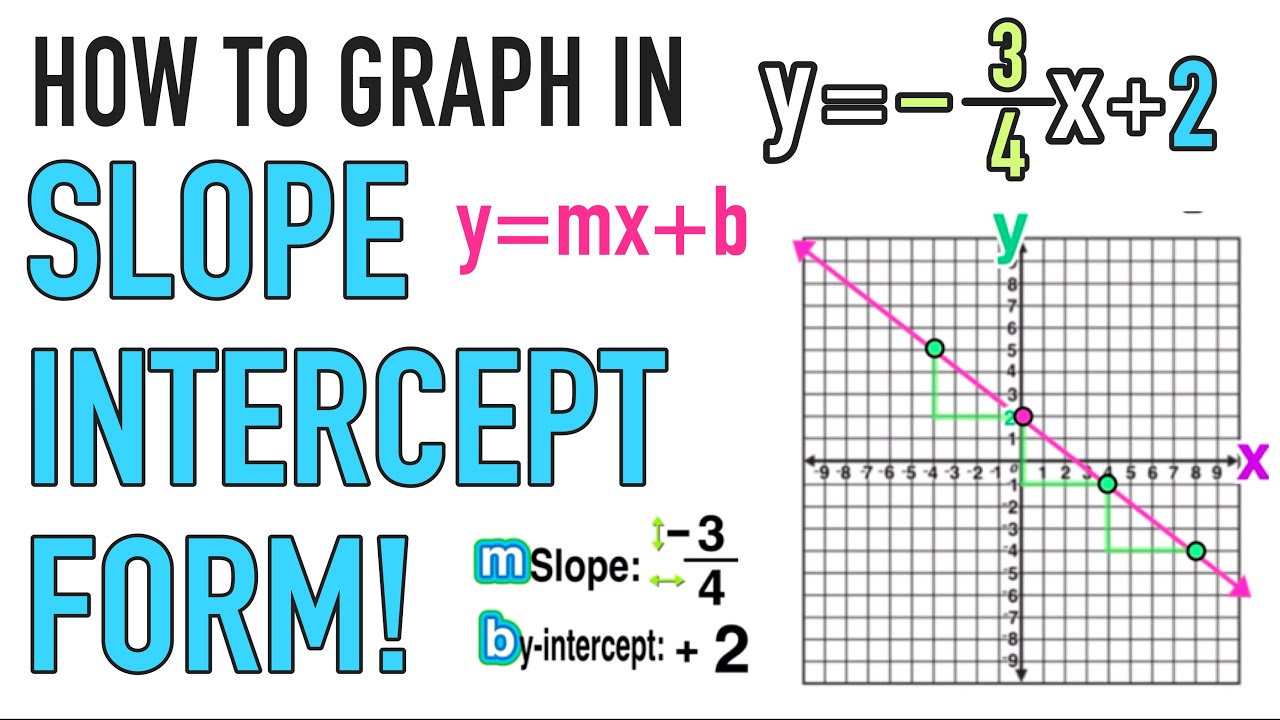
-Step-24-Version-2.jpg)