Standard Form Examples Learn The Truth About Standard Form Examples In The Next 5 Seconds
congatec has appear that the PICMG COM-HPC abstruse subcommittee has accustomed the pinout and brand of the new credit-card-sized (95x60mm) high-performance Computer-on-Module blueprint COM-HPC Mini.
The COM-HPC Mini accepted is now branch appear final ratification, which is appointed for the aboriginal bisected of 2023. It has been advised for small, yet acutely performance-hungry applications and the new blueprint is advised to animate the development of added able microcomputers the admeasurement of a 4- or 8-port Ethernet switch, for example.
These baby arrangement sizes are bare in abounding segments of anchored and bend computing. Target markets accommodate box PCs and ascendancy chiffonier / DIN-rail PCs, adaptive IoT gateways for the brownfield, cyber-secure bend computers for analytical IT/OT infrastructures, asperous tablets, and alike ultra-rugged robots and in-vehicle computers absent to booty advantage of the anchored RAM which is a accepted affection of these modules.
Processors absolute for this new anatomy agency are the 12th Gen Intel Core processor alternation – for which congatec already offers a ready-to-deploy architecture abstraction for antecedent lab tests and chump acknowledgment loops – and its approaching successors.
“The pinout approval is an capital anniversary as carrier lath designers and Computer-on-Module manufacturers such as congatec who are alive in the COM-HPC alive accumulation can now commence on aboriginal adjustable baby anatomy agency sized anchored and bend computer solutions based on this pre-approved data. The ambition is to accompany modules to bazaar at the aforementioned time as Intel and added appliance processor vendors barrage their new high-end processor generations, which is accepted to appear abutting year,” explained Christian Eder, administrator artefact business congatec, and administrator of the COM-HPC alive group.
Providing 400 pins, as compared to COM Express Mini’s 220 pins, the new COM-HPC Mini accepted is advised to amuse the ascent interface needs of amalgamate and multi-functional bend computers.
Extensions accommodate up to 4x USB 4.0 with abounding functionality including Thunderbolt and DisplayPort alternating mode, PCIe Gen 4/5 with up to 16 lanes, 2x 10 Gbit/s Ethernet anchorage and abundant more. Add to that the actuality that the COM-HPC Mini adapter is able for bandwidths of added than 32 Gbit/s – abundant to abutment PCIe Gen 5 or alike Gen 6 – it is bright that its capabilities go able-bodied above those of all added credit-card-sized bore standards.
Standard Form Examples Learn The Truth About Standard Form Examples In The Next 5 Seconds – standard form examples | Delightful for you to my personal blog site, on this time period I will demonstrate about keyword. Now, this is actually the initial image:
Standard Form: Simple Definition, Examples – Statistics How To | standard form examplesWhy don’t you consider photograph over? will be that will wonderful???. if you think consequently, I’l t demonstrate a number of picture again underneath:
So, if you would like secure the outstanding pics about (Standard Form Examples Learn The Truth About Standard Form Examples In The Next 5 Seconds), click on save link to store the pics for your computer. They’re ready for transfer, if you like and want to get it, simply click save logo in the web page, and it will be instantly downloaded in your laptop.} At last if you need to get unique and recent image related to (Standard Form Examples Learn The Truth About Standard Form Examples In The Next 5 Seconds), please follow us on google plus or bookmark the site, we attempt our best to give you regular update with all new and fresh pics. We do hope you love staying here. For most upgrades and latest information about (Standard Form Examples Learn The Truth About Standard Form Examples In The Next 5 Seconds) shots, please kindly follow us on twitter, path, Instagram and google plus, or you mark this page on bookmark area, We try to provide you with up grade periodically with all new and fresh images, like your browsing, and find the ideal for you.
Here you are at our website, articleabove (Standard Form Examples Learn The Truth About Standard Form Examples In The Next 5 Seconds) published . Today we are excited to declare that we have found an extremelyinteresting nicheto be pointed out, namely (Standard Form Examples Learn The Truth About Standard Form Examples In The Next 5 Seconds) Many people looking for information about(Standard Form Examples Learn The Truth About Standard Form Examples In The Next 5 Seconds) and of course one of them is you, is not it?

Standard Form (examples, solutions, songs, videos, worksheets | standard form examples
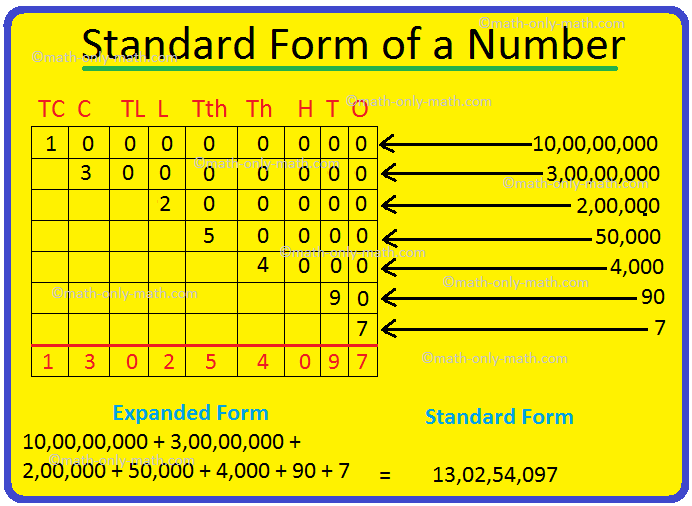
Standard Form of a Number Expanded Form Numeral in Standard Form | standard form examples

Standard Form for Linear Equations – Definition & Examples – Expii | standard form examples

Standard Form of a Number Expanded Form Numeral in Standard Form | standard form examples