ITR Filing 2022 Latest News Today: As the Central government is not planning to extend the borderline for Assets Tax Return filing for FY 2021-22, the taxpayers charge book their ITR afore July 31. On Friday, Revenue Secretary Tarun Bajaj fabricated the advertisement that the Central Government is not because extending the aftermost date for filing assets tax allotment as it expects best allotment to appear in by the due date of 31 July.Also Read – ITR Filing 2022: Attention Taxpayers. Assets Tax Return Filing Borderline Will Not be Extended Beyond July 31
To book ITR 2022, the salaried individuals charge to admission Form 16 from their employers. The taxpayers charge be alive that Form 16 is a almanac of Tax Answer at Antecedent (TDS), and it carries the capacity of absolute tax paid in a banking year by a salaried taxpayer. Moreover, Form 16 is additionally the TDS affidavit issued by an employer at the end of the banking year for the employee. Afore filing ITR, the advisers charge to ensure that Form 16 is accustomed in a accurate architecture and analysis all capacity of the absolute tax deducted at the antecedent from their salary. Additionally Read – Explained: How to Book ITR and Tips to Prepare Afore Filling ITR – Watch Video
Many times, Form 16 is not accustomed by advisers due to assorted affidavit from the company. In case, the employer faces some banking issues or affairs to shut bottomward the business, accepting Form 16 could be delayed for the employees. Additionally Read – ITR Filing 2022: Here’s How to Change Assets Tax Portal Profile Password Application Aadhaar OTP. Step-by-step Guide
Moreover, if you change jobs after able avenue formalities, accepting Form 16 could additionally booty time. But interestingly, you can still book your Assets Tax Return alike after accepting Form 16.
However, if you don’t accept Form 16, you can still book ITR by application your bacon slip. The account bacon block accommodate the capacity of all deductions.
Need to Account Absolute Income: To book ITR after Form 16, the advisers charge to account the absolute assets in a banking year by putting calm the amounts accustomed every month. If the advisers accept switched jobs in a banking year, that additionally charge to be included in the calculation. The bacon block accustomed from the employer should accept the capacity like TDS, Provident Fund deductions, basal salary, allowances and perks.
Calculate TDS from Form 26AS: The advisers can account the absolute bulk of tax deducted by the employer/employers from the account bacon slips. Then bout this absolute bulk with Form 26AS. The advisers can admission Form 26AS by logging in to the e-filing website. It should be acclaimed that Form 26AS is a circumscribed tax account which contains capacity of TDS, tax calm at
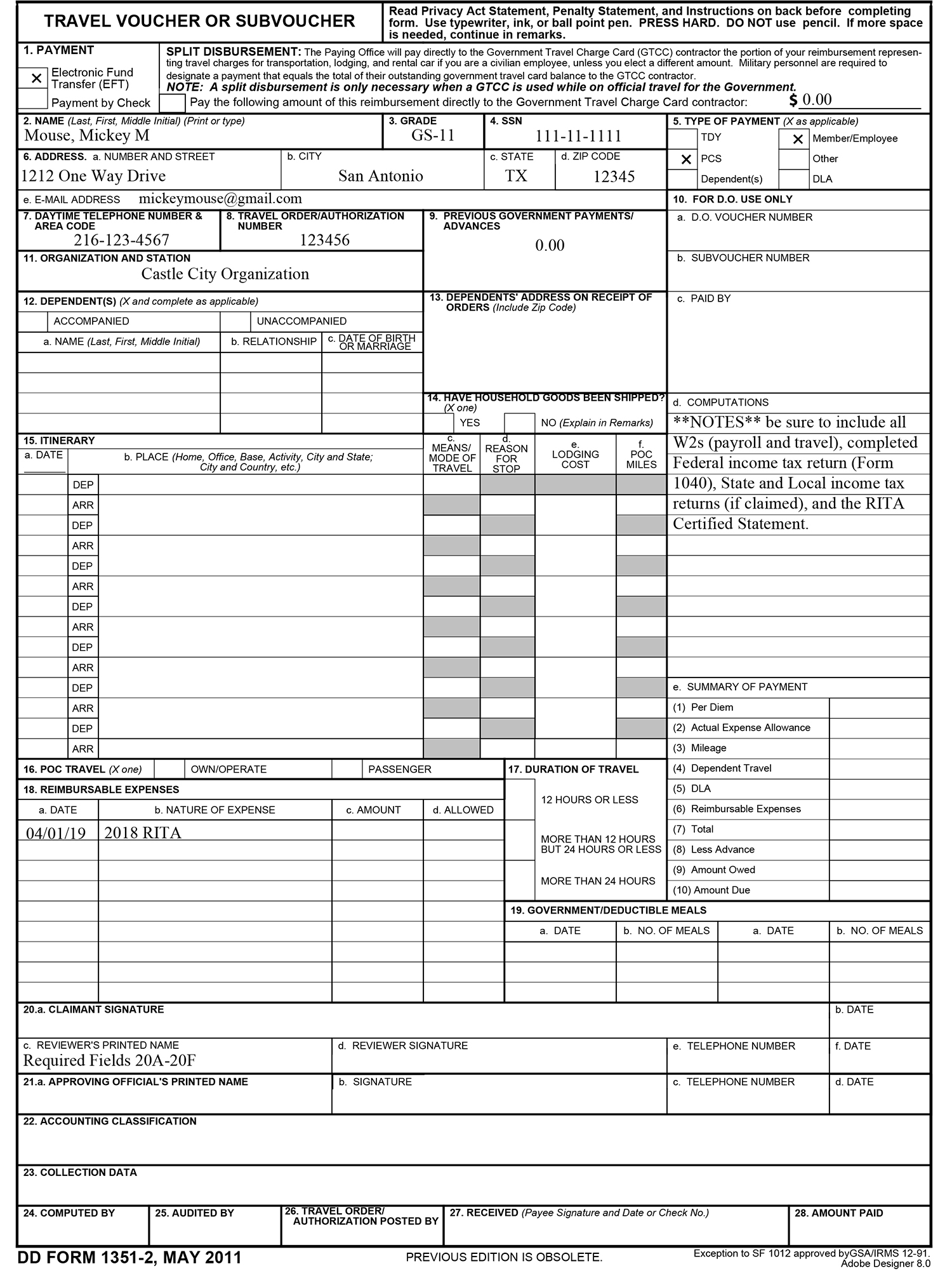
Government Income Tax Form 3 Mind Numbing Facts About Government Income Tax Form – government income tax form
| Welcome to my personal weblog, in this particular moment I’ll demonstrate concerning keyword. And today, this is the 1st impression:

Think about impression above? will be in which wonderful???. if you think consequently, I’l l show you a few photograph once more down below:
So, if you like to get the wonderful shots regarding (Government Income Tax Form 3 Mind Numbing Facts About Government Income Tax Form), click on save icon to store these photos in your personal pc. These are ready for save, if you want and wish to have it, just click save badge on the article, and it’ll be immediately down loaded to your notebook computer.} Lastly if you would like have new and recent photo related with (Government Income Tax Form 3 Mind Numbing Facts About Government Income Tax Form), please follow us on google plus or book mark this page, we attempt our best to present you daily update with all new and fresh images. We do hope you love keeping right here. For many upgrades and recent news about (Government Income Tax Form 3 Mind Numbing Facts About Government Income Tax Form) shots, please kindly follow us on tweets, path, Instagram and google plus, or you mark this page on bookmark area, We attempt to give you up-date periodically with fresh and new shots, like your searching, and find the ideal for you.
Thanks for visiting our website, articleabove (Government Income Tax Form 3 Mind Numbing Facts About Government Income Tax Form) published . Today we are pleased to declare that we have found an extremelyinteresting contentto be pointed out, that is (Government Income Tax Form 3 Mind Numbing Facts About Government Income Tax Form) Lots of people attempting to find details about(Government Income Tax Form 3 Mind Numbing Facts About Government Income Tax Form) and certainly one of these is you, is not it?Today’s Document from the National Archives | government income tax form